Contextures: Representations from Contexts

Despite the empirical success of foundation models, we do not have a systematic characterization of the representations that these models learn. In this paper, we establish the contexture theory. It shows that a large class of representation learning methods can be characterized as learning from the association between the input and a context variable. Specifically, we show that many popular methods aim to approximate the top-d singular functions of the expectation operator induced by the context, in which case we say that the representation learns the contexture. We demonstrate the generality of the contexture theory by proving that representation learning within various learning paradigms -- supervised, self-supervised, and manifold learning -- can all be studied from such a perspective. We also prove that the representations that learn the contexture are optimal on those tasks that are compatible with the context. One important implication of the contexture theory is that once the model is large enough to approximate the top singular functions, further scaling up the model size yields diminishing returns. Therefore, scaling is not all we need, and further improvement requires better contexts. To this end, we study how to evaluate the usefulness of a context without knowing the downstream tasks. We propose a metric and show by experiments that it correlates well with the actual performance of the encoder on many real datasets.

Contextures: The Mechanism of Representation Learning

This dissertation establishes the contexture theory to mathematically characterize the mechanism of representation learning, or pretraining. Despite the remarkable empirical success of foundation models, it is not very clear what representations they learn, and why these representations are useful for various downstream tasks. A scientific understanding of representation learning is critical, especially at this point when scaling up the model size is producing diminishing returns, and designing new pretraining methods is imperative for further progress. Prior work treated different representation learning methods quite differently, whereas the contexture theory provides a unified framework for analyzing these methods. The central argument is that a representation is learned from the association between the input X and a context variable A. We prove that if an encoder captures the maximum information of this association, in which case we say that the encoder learns the contexture, then it will be optimal on the class of tasks that are compatible with the context. We also show that a context is the most useful when the association between X and A is neither too strong nor too weak. The important implication of the contexture theory is that increasing the model size alone will achieve diminishing returns, and further advancements require better contexts. We demonstrate that many pretraining objectives can learn the contexture, including supervised learning, self-supervised learning, generative models, etc. Then, we introduce two general objectives -- SVME and KISE, for learning the contexture. We also show how to mix multiple contexts together, an effortless way to create better contexts from existing ones. Then, we prove statistical learning bounds for representation learning. Finally, we discuss the effect of the data distribution shift from pretraining to the downstream task.

Spectrally Transformed Kernel Regression

Unlabeled data is a key component of modern machine learning. In general, the role of unlabeled data is to impose a form of smoothness, usually from the similarity information encoded in a base kernel, such as the $\epsilon$-neighbor kernel or the adjacency matrix of a graph. This work revisits the classical idea of spectrally transformed kernel regression (STKR), and provides a new class of general and scalable STKR estimators able to leverage unlabeled data. Intuitively, via spectral transformation, STKR exploits the data distribution for which unlabeled data can provide additional information. First, we show that STKR is a principled and general approach, by characterizing a universal type of "target smoothness", and proving that any sufficiently smooth function can be learned by STKR. Second, we provide scalable STKR implementations for the inductive setting and a general transformation function, while prior work is mostly limited to the transductive setting. Third, we derive statistical guarantees for two scenarios: STKR with a known polynomial transformation, and STKR with kernel PCA when the transformation is unknown. Overall, we believe that this work helps deepen our understanding of how to work with unlabeled data, and its generality makes it easier to inspire new methods.

Responsible AI (RAI) Games and Ensembles

Several recent works have studied the societal effects of AI; these include issues such as fairness, robustness, and safety. In many of these objectives, a learner seeks to minimize its worst-case loss over a set of predefined distributions (known as uncertainty sets), with usual examples being perturbed versions of the empirical distribution. In other words, aforementioned problems can be written as min-max problems over these uncertainty sets. In this work, we provide a general framework for studying these problems, which we refer to as Responsible AI (RAI) games. We provide two classes of algorithms for solving these games: (a) game-play based algorithms, and (b) greedy stagewise estimation algorithms. The former class is motivated by online learning and game theory, whereas the latter class is motivated by the classical statistical literature on boosting, and regression. We empirically demonstrate the applicability and competitive performance of our techniques for solving several RAI problems, particularly around subpopulation shift.

Understanding Augmentation-based Self-Supervised Representation Learning via RKHS Approximation

Good data augmentation is one of the key factors that lead to the empirical success of self-supervised representation learning such as contrastive learning and masked language modeling, yet theoretical understanding of its role in learning good representations remains limited. Recent work has built the connection between self-supervised learning and approximating the top eigenspace of a graph Laplacian operator. Learning a linear probe on top of such features can naturally be connected to RKHS regression. In this work, we use this insight to perform a statistical analysis of augmentation-based pretraining. We start from the isometry property, a key geometric characterization of the target function given by the augmentation. Our first main theorem provides, for an arbitrary encoder, near tight bounds for both the estimation error incurred by fitting the linear probe on top of the encoder, and the approximation error entailed by the fitness of the RKHS the encoder learns. Our second main theorem specifically addresses the case where the encoder extracts the top-d eigenspace of a Monte-Carlo approximation of the underlying kernel with the finite pretraining samples. Our analysis completely disentangles the effects of the model and the augmentation. A key ingredient in our analysis is the augmentation complexity, which we use to quantitatively compare different augmentations and analyze their impact on downstream performance on synthetic and real datasets.

Characterizing Out-of-Distribution Error via Optimal Transport

Out-of-distribution (OOD) data poses serious challenges in deployed machine learning models, so methods of predicting a model's performance on OOD data without labels are important for machine learning safety. While a number of methods have been proposed by prior work, they often underestimate the actual error, sometimes by a large margin, which greatly impacts their applicability to real tasks. In this work, we identify pseudo-label shift, or the difference between the predicted and true OOD label distributions, as a key indicator to this underestimation. Based on this observation, we introduce a novel method for estimating model performance by leveraging optimal transport theory, Confidence Optimal Transport (COT), and show that it provably provides more robust error estimates in the presence of pseudo-label shift. Additionally, we introduce an empirically-motivated variant of COT, Confidence Optimal Transport with Thresholding (COTT), which applies thresholding to the individual transport costs and further improves the accuracy of COT's error estimates. We evaluate COT and COTT on a variety of standard benchmarks that induce various types of distribution shift -- synthetic, novel subpopulation, and natural -- and show that our approaches significantly outperform existing state-of-the-art methods with an up to 3x lower prediction error.

Predicting Out-of-Distribution Error with Confidence Optimal Transport

Out-of-distribution (OOD) data poses serious challenges in deployed machine learning models as even subtle changes could incur significant performance drops. Being able to estimate a model's performance on test data is important in practice as it indicates when to trust to model's decisions. We present a simple yet effective method to predict a model's performance on an unknown distribution without any addition annotation. Our approach is rooted in the Optimal Transport theory, viewing test samples' output softmax scores from deep neural networks as empirical samples from an unknown distribution. We show that our method, Confidence Optimal Transport (COT), provides robust estimates of a model's performance on a target domain. Despite its simplicity, our method achieves state-of-the-art results on three benchmark datasets and outperforms existing methods by a large margin.

Understanding Why Generalized Reweighting Does Not Improve Over ERM

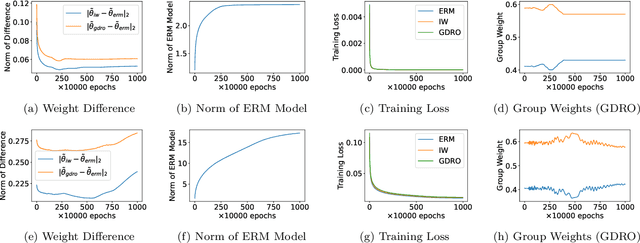
Empirical risk minimization (ERM) is known in practice to be non-robust to distributional shift where the training and the test distributions are different. A suite of approaches, such as importance weighting, and variants of distributionally robust optimization (DRO), have been proposed to solve this problem. But a line of recent work has empirically shown that these approaches do not significantly improve over ERM in real applications with distribution shift. The goal of this work is to obtain a comprehensive theoretical understanding of this intriguing phenomenon. We first posit the class of Generalized Reweighting (GRW) algorithms, as a broad category of approaches that iteratively update model parameters based on iterative reweighting of the training samples. We show that when overparameterized models are trained under GRW, the resulting models are close to that obtained by ERM. We also show that adding small regularization which does not greatly affect the empirical training accuracy does not help. Together, our results show that a broad category of what we term GRW approaches are not able to achieve distributionally robust generalization. Our work thus has the following sobering takeaway: to make progress towards distributionally robust generalization, we either have to develop non-GRW approaches, or perhaps devise novel classification/regression loss functions that are adapted to the class of GRW approaches.

Boosted CVaR Classification

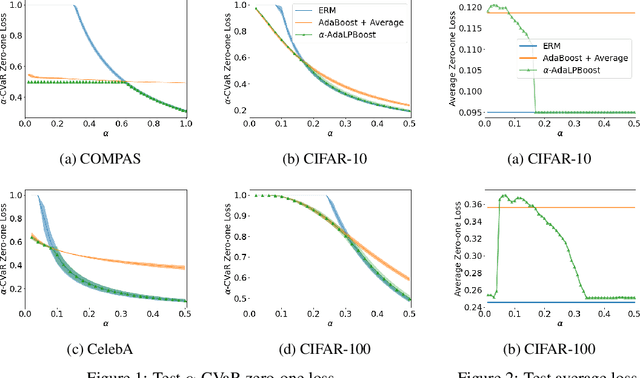
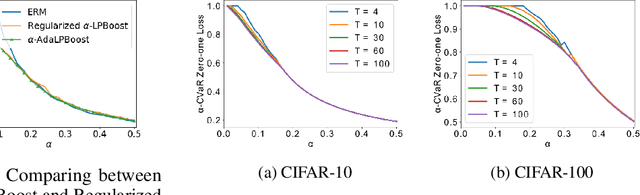
Many modern machine learning tasks require models with high tail performance, i.e. high performance over the worst-off samples in the dataset. This problem has been widely studied in fields such as algorithmic fairness, class imbalance, and risk-sensitive decision making. A popular approach to maximize the model's tail performance is to minimize the CVaR (Conditional Value at Risk) loss, which computes the average risk over the tails of the loss. However, for classification tasks where models are evaluated by the zero-one loss, we show that if the classifiers are deterministic, then the minimizer of the average zero-one loss also minimizes the CVaR zero-one loss, suggesting that CVaR loss minimization is not helpful without additional assumptions. We circumvent this negative result by minimizing the CVaR loss over randomized classifiers, for which the minimizers of the average zero-one loss and the CVaR zero-one loss are no longer the same, so minimizing the latter can lead to better tail performance. To learn such randomized classifiers, we propose the Boosted CVaR Classification framework which is motivated by a direct relationship between CVaR and a classical boosting algorithm called LPBoost. Based on this framework, we design an algorithm called $\alpha$-AdaLPBoost. We empirically evaluate our proposed algorithm on four benchmark datasets and show that it achieves higher tail performance than deterministic model training methods.

DORO: Distributional and Outlier Robust Optimization

Many machine learning tasks involve subpopulation shift where the testing data distribution is a subpopulation of the training distribution. For such settings, a line of recent work has proposed the use of a variant of empirical risk minimization(ERM) known as distributionally robust optimization (DRO). In this work, we apply DRO to real, large-scale tasks with subpopulation shift, and observe that DRO performs relatively poorly, and moreover has severe instability. We identify one direct cause of this phenomenon: sensitivity of DRO to outliers in the datasets. To resolve this issue, we propose the framework of DORO, for Distributional and Outlier Robust Optimization. At the core of this approach is a refined risk function which prevents DRO from overfitting to potential outliers. We instantiate DORO for the Cressie-Read family of R\'enyi divergence, and delve into two specific instances of this family: CVaR and $\chi^2$-DRO. We theoretically prove the effectiveness of the proposed method, and empirically show that DORO improves the performance and stability of DRO with experiments on large modern datasets, thereby positively addressing the open question raised by Hashimoto et al., 2018.